Aunque el principio de Arquímedes fue introducido como principio, de hecho puede considerarse un teorema demostrable a partir de las ecuaciones de Navier-Stokes para un fluido en reposo, mediante el teorema de Stokes igualmente el principio de Arquímedes puede deducirse matemáticamente de las ecuaciones de Euler para un fluido en reposo que a su vez pueden deducirse generalizando las leyes de Newton a un medio continuo. Partiendo de las ecuaciones de Navier-Stokes para un fluido:
(1)
![\rho_f\left[\frac{\part\mathbf{v}}{\part t} +\mathbf{v}(\boldsymbol\nabla\cdot \mathbf{v})\right]= \mu\Delta\mathbf{v} - \boldsymbol\nabla p + \rho_f\mathbf{g}](http://upload.wikimedia.org/math/e/3/9/e393441851465232f8640c2b0f42b3e1.png)
La condición de que el fluido incompresible que esté en reposo implica tomar en la ecuación anterior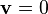 
, lo que permite llegar a la relación fundamental entre presión del fluido, densidad del fluido y aceleración de la gravedad:
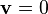, lo que permite llegar a la relación fundamental entre presión del fluido, densidad del fluido y aceleración de la gravedad:(2)
A partir de esa relación podemos reescribir fácilmente las fuerzas sobre un cuerpo sumergido en términos del peso del fluido desalojado por el cuerpo. Cuando se sumerge un sólido K en un fluido, en cada punto de su superficie aparece una fuerza por unidad de superfice 
perpendicular a la superficie en ese punto y proporcional a la presión del fluido pen ese punto. Si llamamos 
al vector normal a la superficie del cuerpo podemos escribir la resultante de las fuerzas 
sencillamente mediante el teorema de Stokes de la divergencia:
perpendicular a la superficie en ese punto y proporcional a la presión del fluido pen ese punto. Si llamamos al vector normal a la superficie del cuerpo podemos escribir la resultante de las fuerzas sencillamente mediante el teorema de Stokes de la divergencia:(3)
Donde la última igualdad se da sólo si el fluido es incompresible.
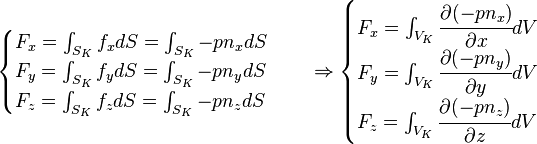
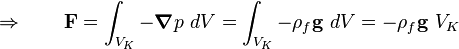
Tomaron todo esto de wikipedia, y no referenciaron.
ResponderEliminar